https://www.acmicpc.net/problem/1041
1041번: 주사위
첫째 줄에 N이 주어진다. 둘째 줄에 주사위에 쓰여 있는 수가 주어진다. 위의 그림에서 A, B, C, D, E, F에 쓰여 있는 수가 차례대로 주어진다. N은 1,000,000보다 작거나 같은 자연수이고, 쓰여 있는 수
www.acmicpc.net
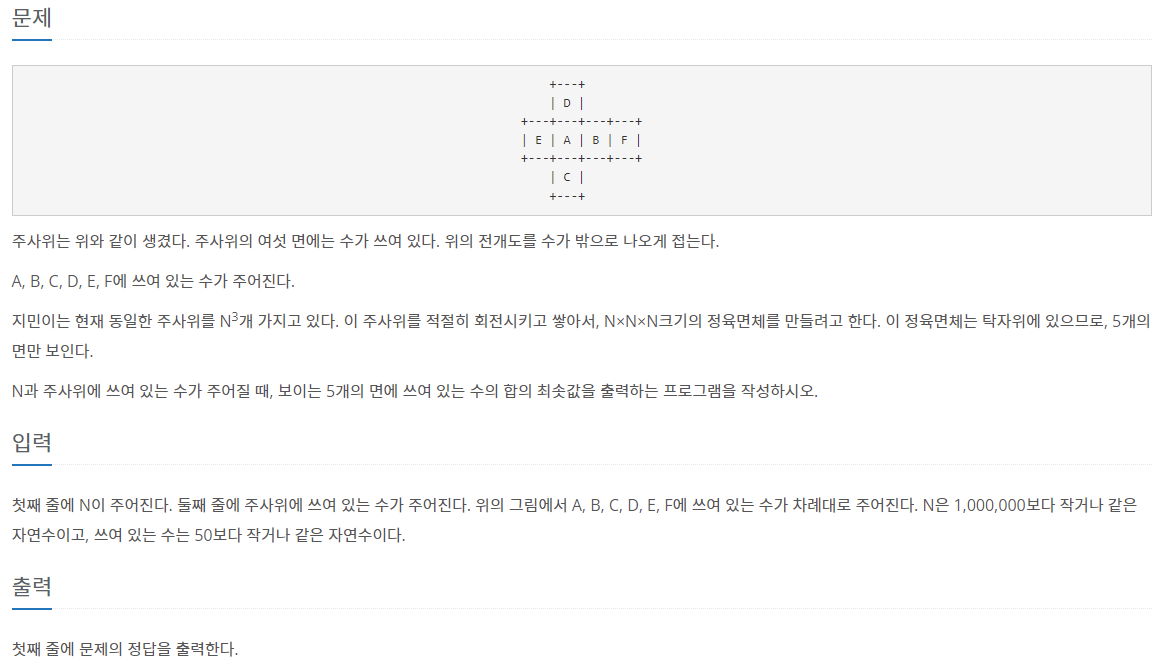
문제 해석
주사위를 n^3 크기의 정육면체로 만드는데 바닥을 제외한 5면의 최소값을 구하는 문제이다.
코드
# BOJ 1041
n = int(input())
dice = list(map(int, input().split()))
a, b, c, d, e, f = dice[0], dice[1], dice[2], dice[3], dice[4], dice[5]
# 한 면이 보일 때 최소값
min1 = min(dice)
# 두 면이 보일 때 최소값
side_2 = [(a, b), (a, c), (a, d), (a, e), (b, d), (e, d), (e, c), (c, b), (d, f), (b, f), (c, f), (e, f)]
min2 = sum(side_2[0])
for i, j in side_2:
min2 = min(min2, i + j)
# 세 면이 보일 때 최소값
side_3 = [(a, b, c), (a, c, e), (a, d, b), (a, e, d), (d, f, b), (b, f, c), (c, f, e), (e, f, d)]
min3 = sum(side_3[0])
for i, j, k in side_3:
min3 = min(min3, i + j + k)
# 각 면이 보일때 갯수 만큼 더하기
ans = 0
ans += (4 * (n - 1) * (n - 2) + (n - 2) * (n - 2)) * min1
ans += ((n - 1) * 4 + (n - 2) * 4) * min2
ans += 4 * min3
# n 이 1이라면 모든 면 - 가장 숫자가 높은면
if n == 1: ans = sum(dice) - max(dice)
print(ans)문제 풀이
이번 문제도 그려서 생각해보는것이 좋다!
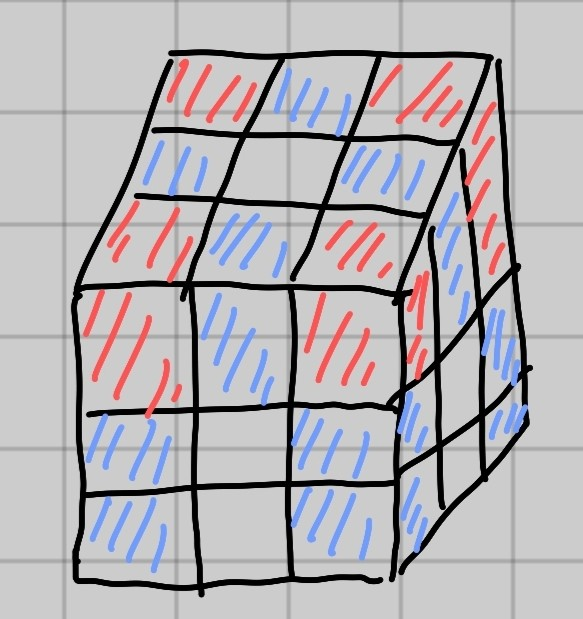
다음은 n = 3인 경우의 정육면체를 그려보았다.
여기서 알 수 있는 것으로 색을 칠하지 않은 칸은 면이 한 면만 보인 경우이다.
이 경우엔 옆면이 4면 X 두칸 차지하고 있으므로 (n - 2) * (n - 1)이 되고 윗면에 (n - 2) * (n - 2)가 된다.
다음은 두 면이 보이는 경우이다.
겹치지 않도록 생각해야 하므로 윗면에는 (n - 2) * 4가 되고, 밑면에는 (n - 1 ) * 4가된다.
다음은 세 면이 보이는 경우이다.
이 경우는 4개의 경우 뿐이다.
따라서 이 경우에 한 면이 보일 때 최소값, 두 면이 보일 때 최소값, 세 면이 보일 때 최소값을 찾아 곱해주면 된다.
주사위에 따라 보여지는 면은 정해져 있기 때문에 해당 면을 모두 나열하여 배열에 넣어 최소값을 구해주었다.
'알고리즘 > BOJ' 카테고리의 다른 글
| [BOJ/python] 13460번 구슬 탈출 2 (0) | 2022.07.20 |
|---|---|
| [BOJ/python] 2096번 내려가기 (0) | 2022.07.09 |
| [BOJ/python] 1149번 RGB거리 (0) | 2022.07.08 |
| [BOJ/python] 14890번 경사로 (0) | 2022.07.01 |
| [BOJ/python] 14499번 주사위 굴리기 (0) | 2022.07.01 |
